Project: Symbolic, Rational-coefficient, Polynomial Algebra
In one of my circuits courses at CMU, I remember having to perform Partial Fraction Decomposition on a few basic quadratic or cubic polynomials. Because the way to do partial fraction decomposition is so straight-forward, or programmatic, I naturally wanted to write a program to do that for me. However, I heavily under-estimated the difficulty of finding roots for an arbitrary polynomial. I'm still working on writing the partial fraction decomposition engine, but I finished writing a tool which would do polynomial arithmetic.
Neither the complexity nor the usefulness of this app were particularly impressive, but all together it was a really good programming exercise. To make my job even easier, I decided that I'm only going to work with real, rational-valued coefficient polynomials. Here are a couple questions that I had to answer before I could start coding:
- How can I represent a polynomial?
- What is an algorithm which will multiply polynomials? Is this easy to do with the representation you chose?
- What is polynomial long division? How does it work?
- What is a good polynomial factoring algorithm? (Still working on the answer to this... see the "LLL" algorithm)
Another front-end challenge was getting polynomials to render properly in Java. I tried to look for a LaTeX plugin of some sort, but gave up after about a half an hour of looking. If you know a good Math Visualization package for Java, let me know. I ended up writing my own Swing library for this, but it's very limited and really only renders ratios.
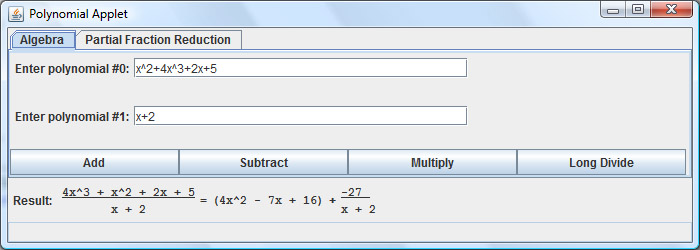
Click to run the Java .jar executable. Only rational coefficients supported. Ex: 5/3x^2+2x-1